Wachstum, Grenzen, Chaos

Der Wahnsinn des Wachstums

Bäume wachsen nicht in den Himmel.
lehrt eine alte Volksweisheit. Trotzdem versucht der Mensch gerne immer mal wieder sich am Beweis des Gegenteils eine blutige Nase zu holen.

Wachstumsprozesse wie Bakterienkulturen, Zinseszinsen oder Bruttosozialprodukte – auch junge Bäume – folgen grob den Gesetzen vom exponentiellen Wachstum.

In der Vereinfachung – mit festen, abgegrenzten Zeitschritten – wird das durch eine geometrische Reihe beschrieben. Diese ist dadurch festgelegt, daß der Folgewert immer um durch einen Faktor (oder einen Prozentsatz, was nur eine andere Schreibweise ist) aus dem Wert einer Periode vorher ermittelt wird.

Solche Wachstumsvorgänge enden immer, auch wenn sie anfangs sehr klein und unbedeutend erscheinen, in einem explosionsartigen Verlauf, der alle gesetzten Grenzen in kurzer Zeit überschreitet.

Bekannte Beispiele:

Seerosenteich

Jeden Tag verdoppelt sich die Fläche der Seerosen. Auch wenn Anfangs die bedeckte Fläche nur klein ist, und es lange dauert, bis der Teich halb zugewachsen ist, dauert es nur einen weiteren Tag, bis der Teich komplett zu ist.

Templergold

Hätten die Tempelritter, als sie im 14. Jahrhundert aufgelöst wurden, ihr Goldvermögen in Sicherheit gebracht und mit 5% Verzinsung jährlich gut angelegt, würde heute das ganze auf der Welt verfügbare Gold nicht ausreichen, dieses Vermögen zu decken.

Josefspfennig
Reiskörner auf dem Schachbrett

Rindvieh

Wenn ein Landwirt „mithalten” will, muß er ständig wachsen.
Bei den Milchkühen hat sich z. B. der „Zukunftsbetrieb” in den letzten 50 Jahren alle 20 Jahre verdoppelt.
Das entspricht 3,5 % mehr jedes Jahr.
Das klingt nach nicht viel. Eine Kuh macht Muh, viele Kühe machen Mühe.
Trotz Melkroboter und großer Technik ist Milchvieh immer noch arbeitsintensiv.
Da kann man nicht einfach mal 'ne Mio drauf schmeißen und dann läuft alles von alleine.
Trotzdem:
Würde ich heute für Kühe neu bauen, müßte ich für ca 100 Kühe bauen.

Mein Hof ist seit über 300 Jahren in ununterbrochen nachgewiesenem Familienbesitz.
Sollte dieser Hof auch die nächsten 300 Jahre eine Familie ernähren, – müßten dann meine Nachfolger auch alle 20 Jahre, also 15 mal, den Bestand verdoppeln? Im Jahre 2310 stünden dann
100 * 2¹⁵ = 3.276.800 — 3 Millionen Kühe im Stall.
Milchsee?

Keine Gesellschaftsordnung hat mehr Menschen um ihre eigenständige Existenz gebracht als die sogenannte „freie Marktwirtschaft”.
Bolschewistische Verbrecherbande?

Der gegarte Frosch

Wie gart man einen Frosch?

Ähnlich ist es mit dem Wahnsinn des Zinses.
Die Auswirkungen innerhalb einer Generation werden durchaus noch als angenehm empfunden.

     1,05 ²⁵ = 3,4 → „Es geht uns doch wirklich gut.”

Über ein Menschenleben hinweg wird das schon kritischer gesehen.
Wer kennt nicht die Zweifel der „Alten”:

     1,05 ⁷⁵ = 39 → „…wo das wohl noch alles hinführen wird…”

In historsichen Dimensionen von Staaten und Systemen, wo Kriege und Revolutionen wachsen, gibt es kein persönliches Gefühl mehr, nur mehr verkopftes Bücherlesen.

     1,05 ²⁰⁰ = 17 300 → „Die Welt ist zu klein für uns.”

Die Weisheiten zum Verständis chaotischer Systeme finden sich aber durchaus schon in antiken Überlieferungen. Es wäre eine interessante Fleißaufgabe, das Alte Testament danach zu durchforschen.

Haben Sie Merkels Kommentare zur Neuverschuldung noch in Erinnerung?
Nein, sagt die Frau Bundeskanzlerin. Es ist überhaupt nicht heiß. Ich finde es sogar angenehm warm hier.
Quaaak …

Das kleine Einmaleins des Schicksals: Grenzen des Wachstums

Bäume wachsen nicht in den Himmel.
Es gibt eine Grenze, die spürbar wird, wenn man dem Himmel nahe kommt.
(vgl. Turm v. Babel, Ikarus-Sage, fette / magere Jahre).

Die logistische Gleichung wurde ursprünglich 1837 von Pierre François Verhulst als demografisches Modell eingeführt. Die Gleichung ist ein Beispiel dafür, wie komplexes, chaotisches Verhalten aus einfachen nichtlinearen Gleichungen entstehen kann.

Das logistische Modell berücksichtigt zwei Einflüsse:

• Wachstum (geometrisch) – z. B. durch Fortpflanzung, Verzinsung, Wirtschaftswachstum…
• Begrenzung – z. B. Verhungern, Währungsreform, Krieg… (Grenzen des Wachstums)

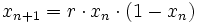
Quelle: Wikipedia

Theorie ist schön, Vertrauen ist gut, selber nachrechnen ist besser.

Tabellen zum selber probieren:

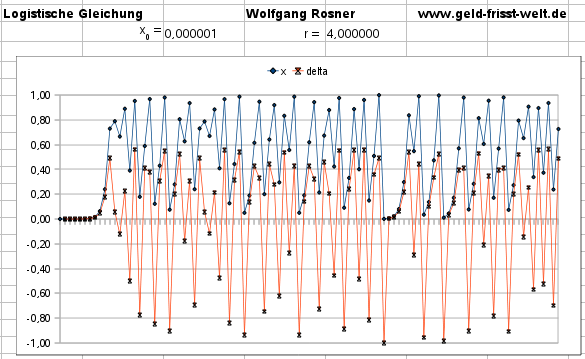
In der Tabelle wird die oben angegene Gleichung jeweils für 100 Schritte berechnet. Blau sind die x_n-Werte, rot („delta”) jeweils die Differenz des aktuellen zum vorhergehenden x-Wert.

Wir spielen vor allem mit dem r-Wert – quasi die Wachstumsdynamik.
Interessant sind vor allem sehr kleine x₀-Werte, um das "Wegwachsen" vom Start weg zu zeigen.
Mehr Parameter gibt es nicht.

Für r < 1 gibt es kein Wachstum, die Population stirbt immer aus.

Für r zwischen 1 … 2 pendelt sich die Population schnell auf einen niedrigen stabilen Wert ein,
was man aber nur bei größeren Startwerten sieht:

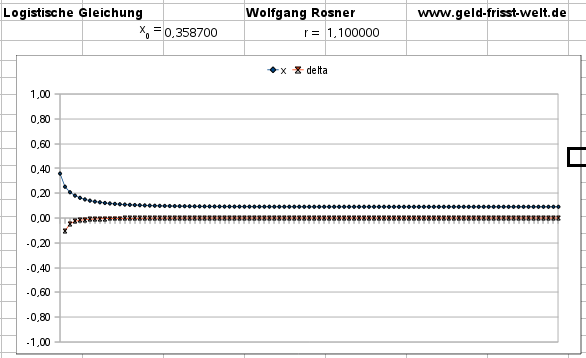
Für r ~ 2 gibt es schon – selbst bei sehr kleinen Startwerten –
zügiges Wachstum zu einem hohen Level hin,
der schnell erreicht und stabil gehalten wird:

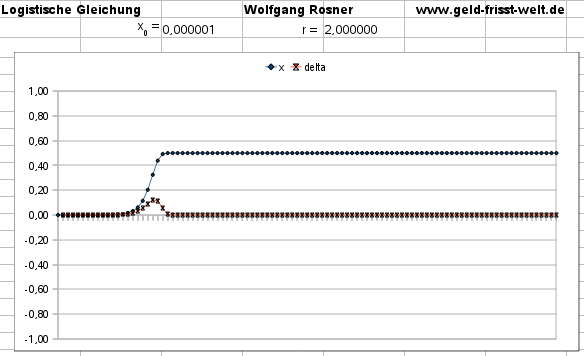
Für r ~ 3 zeigt sich ein „Überschießen” am Ende der Wachstumsphase,
es treten erstmals ”Rezessionsphasen” auf und danach Schwingungen,
letztendlich wird aber doch noch ein stabiler Zustand angenähert:

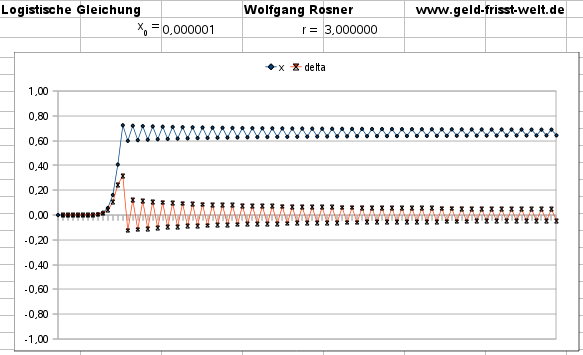
Bereits kleine Steigerungen in der Wachstumsdynamik ändern das Verhalten deutlich.
Bei r ~ 3,2 schaukeln sich Schwingungen auf, die dauerhaft bestehen bleiben:

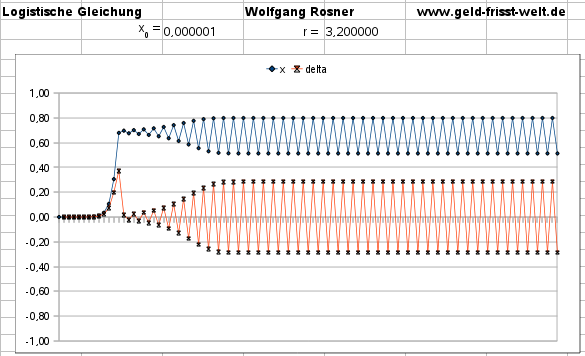
Bei r ~ 3,5 beginnen die Endpunkten der Schwingungen auch, sich zu ändern:

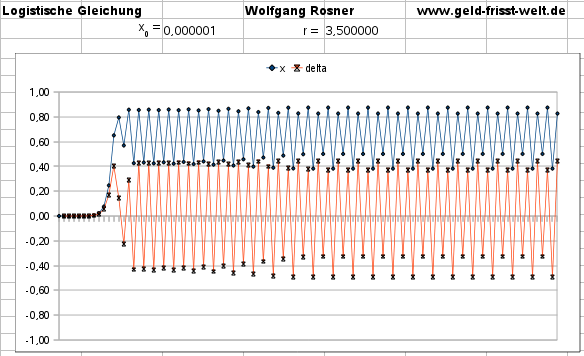
Bei r ~ 3,7 verlieren auch die Schwingungen der Endpunkte ihre stabile Periodizität.
Eine Vorhersage der Zukunft aus Gegenwart und Vergangenheit wird zunehmend unmöglich:

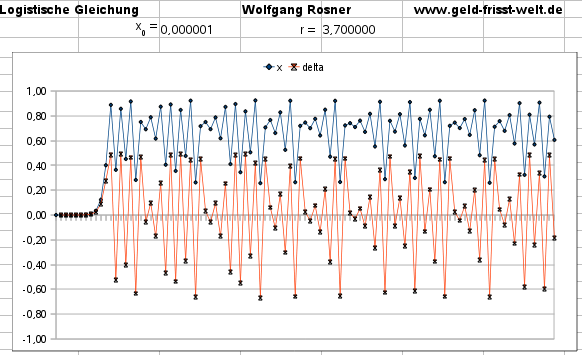
Bei r → 4,0 wird das Chaos perfekt.
Prognosen für die Zukunft werden unmöglich. Sehr turbulente wechseln sich mit nicht ganz so turbulenten Phasen ab.
Manchmal bricht die Population fast vollständig zusammen, ohne daß man das an den Perioden davor hätte erkennen können.
Nach einem massiven Zusammenbruch folgt eine Zeit lang ruhiges, exponentielles Wachstum:

Nochmal: wir haben nichts an der Gleichung selbst geändert. Es ist kein Zufallsgenerator oder irgend eine wüste Funktion eingebaut. Es wird immer nur der nächste Schritt aus dem vorher gehenden nach der oben stehenden einfachen logistischen Formel berechnet. Die Formeln in der Tabelle sind alle die selben. „Das System” ist sozusagen immer einfach und immer das selbe. Das einzige, was sich ändert, ist der Wert r – die Wachstumsdynamik.

Ich möchte Ludwig Erhard und seine Verdienste um die soziale Marktwirtschaft nicht schmälern. Aber bei der Bewertung sollte man immer im Hinterkopf halten, daß das auf Basis einer großen „Abwrackaktion” von 1938 bis 1946 erfolgt ist. Die Ähnlichkeit der Muster ist zumindest frappierend.

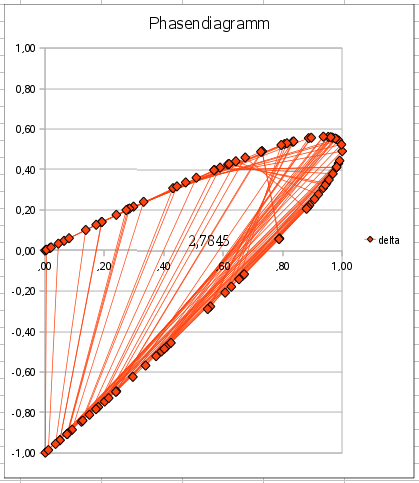
In der Tabelle ist auch noch eine Graphik eingebaut, die delta – also die Änderung der Werte – über die Werte x selbst aufträgt: das Phasendiagramm. Daran erkennt man durchaus ein Muster: alle Punkte liegen auf einer Kurve, die eine Parabel sein könnte, und auch die Verbindungslinien – die Wege von einem Punkt zum nächsten – scheinen ein Muster zu zeigen. Das gibt Anlaß zur Hoffnung, daß das System vielleicht doch nicht so bösartig ist wie es auf Anhieb scheint. Vielleicht läßt sich mit etwas mehr Verständnis wieder eine Prognose riskieren, und im Weiteren sogar eine gezielte Beeinflussung durch geeignete Steuerungsmaßnahmen.

Natürlich ist die logistische Gleichung nur ein sehr einfaches Modell für die komplexe wirschaftliche Realität.
Aber das Grundprinzip:

wird an diesem einfachen System bereits sehr gut deutlich.

Sandkastenmathematik

Quelle: nature.com

Wenn nun dieser Parameter r so kritisch ist, wer stellt den dann ein?
Wo kommt der her?
Können wir den nicht einfach zurückdrehen?
Nun, es gibt Systeme, die bringen sich selber immer wieder „an den Rand des Wahnsinns” &ndash hier ein Beispiel:

Die Anwendung der Chaos-Theorie auf soziale Systeme wird z. B. von Kron näher ausgeführt. Hier zeigt er unter anderem ein Potenzgesetz für die Häufigkeitsverteilung von Kriegstoten – womit aus einem Sandkastenspiel wieder einmal ganz schnell tödlicher Ernst wird.
Vor diesem Hintergrund bekommt Des Teufels Meisterwerk – der Text entstand, bevor ich den Kron-Artikel gesehe hatte – erschreckenden Realitätsbezug.

Zufall oder Chaos?

Für den Uneingeweihten macht das keinen Unterschied.
Wenn man den Verlauf der logistischen Gleichung im voll ausgebildeten Chaos ansieht, könnte man auf den ersten Blick glauben, diese Werte könnten genauso gut ausgewürfelt worden sein.

Doch der Blick auf das Phasendiagramm zeigt, daß eine Gesetzmäßigkeit im System, hier also in der Formel, vorliegt. Wären die einzelnen Punkte zufällig gewürfelt, wäre das Phasendiagramm eine Wolke, und die Verbindungslinien würden kreuz und quer laufen wie die Spur einer verirrten Fliege.

Ein weiterer Fingerabdruck chaotischer Prozesse ist sind die erwähnten Potenzgesetze.
Bei zufälligen Prozessen häufen sich die Meßgrößen um einen Mittelwert, größere und kleinere Werte nehmen in der Häufigkeit ab. Sehr oft – wenn nicht einzelne Effekte dominieren oder sich gegenseitig beeinflussen – hat die Häufigkeitsverteilung die Form der Gauß'schen Glockenkurve.
Chaotische Porzesse zeigen dagegen viele kleine und weniger große Schwankungen in eben der charakteristischen Potenzverteilung auf.

So what –
mag der gelangweilte Leser jetzt fragen – was kümmert's mich?

Spätestens wenn ich anfange, ein System zu managen, ist diese Frage wesentlich – quasi kriegsentscheidend, um im Manager-Slang zu bleiben. Ein zufällig gestörtes System kann ich beruhigen, indem ich Störeinflüsse von außen abschirme. Das erfordert möglicherweise starke Maßnahmen, aber wenn die Störquellen richtig identifizert sind, dann hilfts.

Bei einem chaotischen System bringt eine Abschirmung nach außen gar nichts. Das Chaos kommt ja aus der Struktur selbst von innen heraus. Oft ist es sogar schädlich, die Wirkung des Schadens aufhalten zu wollen. So hat man früher Lawinenzäune gebaut, um Bergdörfer zu schonen. Das Ergebnis war, daß Lawinenabgänge nun zwar seltener, aber dafür dann um so heftiger geworden sind, weil die aufgestaute Schneemasse viel höher war. Heute nimmt man in Skigebieten sogar gezielte Sprengungen vor, um Lawinenabgänge kontrolliert zu provozieren, bevor sich tödliche Massen aufstauen und unkontrolliert abgehen. Aus einer einfachen, linearen Ursache-Wirkungs-Denke heraus wurde diese Maßnahme anfangs oft als unsinnig kritisiert, hat sich aber inzwischen tausendfach bewährt.

Ähnlich verhält es sich mit sozialen Systemen.
„Ausländer raus”, „Grenzen zu”, „Zocker ins Gefängnis” sind lineardenkerische Schnellschußhandlungen, die nur das Symptom bekämpfen, aber nicht die Ursache.
„Wenn's der nicht macht, dann macht's ein Anderer” ist die durchaus weise Antwort des Volksmundes. So lange „man's weiterhin so macht”, wird das gleiche Ergebnis raus kommen, selbst wenn Köpfe rollen.

Die Deutsche Wiedervereinigung hat zwar viel Geld gekostet, aber noch mehr Absatzmärkte gebracht. Es gibt durchaus ernst zu nehmende Stimmen, nach denen durch die wirtschaftliche Wiedervereinigung in Deutschland der Zusammenbruch hinausgeschoben bzw., wie aktuell ja durchaus nachvollziehbar, die wirtschaftliche Position gestärkt wurde.

Wachstum und Grenzen in der Wirtschaft

Die Kräfte in der realen Welt sind natürlich etwas komplexer als im einfachen Beispiel.
Als Wachstumstreiber kommen z. B. in Frage:

• Zunehmender Bedarf aus Menschenmenge x Lifestyle
• Umwälzungen des Status Quo durch Segungen der menschlichen Kreativität
• Zunehmendes Angebot durch Rationalisierungsinvestitionen (=Realkapital)
• die Vollbeschäftigungsforderung als „marktkonforme” Antwort auf die Verteilungsfrage
• unersättliche Gier als Relikt unserer evolutionären Prädisposition
• die Renditeerwartung (=Zinseszins) eines permanent exponentiell intrinsisch wachsenden Bestandes an Finanz(=Imaginär-)kapital

Als Wachstumsbegrenzer wäre z. B. zu erwägen:

• Sättigung des Bedarfs
• Ausgrenzen von Nachfragern durch Versagen der Verteilungsmechanismen („Hunger”)
• begrenzte natürliche Ressourcen und Belastungskapazität
• Mißmanagement in der globalen Bananenrepublik
• Vernichten von Werten wie Ressourcen, Güter, Motivation durch fehlgeleiteten Selektionsmechanismus
• Psychologische Rückwirkungen bei fallenden Zukunftserwartungen

Nur wenn diese Kräfte im Sinne eines „Tunings” ausbalanciert, aufeinander abgestimmt sind, sind stabile Rahmenbedingungen für ein erfolgreiches, effektives und effizientes Wirtschaften gegeben.

Mangels Verständnis und offensichtlich auch Willens seitens der Profiteure der aktuellen Mißwirtschaft steht derzeit jedoch mehr das Wegdiskutieren, Verdrängen und Gesundbeten im Vordergrund.

Erste weiterführende Überlegungen dazu habe ich hier zusammengestellt.
Weiteres wird sicher auf dieser Seite noch folgen.

Für den interessierten Einsteiger, der sich vor allem für Verstehen und Tun, weniger um mathematische Details interessiert, sei Senges Fifth Discipline empfohlen, das sicher auch in deutscher Übersetzung verfübar sein dürfte.